分布式系统-2-同步网络Leader选举算法

引言

在前一篇文章概述中，提到了分布式系统模型大致分类为同步网络模型、异步共享存储器模型、异步网络模型和部分同步模型。今天开始，将慢慢介绍同步网络模型的一些算法，因为同步网络模型有一些严格的环境假设，所以同步网络模型算法比较简单，但是同步网络模型是一个理想化模型，现实生活中这种模型是非常少的，但是学习它们也有助于我们理解后边的异步模型算法和部分同步模型，在接下来的几篇文章中，将分别介绍分布式领域中比较热门的话题包括Leader选举、一致性（包括著名的Byzantine故障下的一致性）、最小生成树和最短路径等问题

先从Leader选举开始

概念准备

网络表示

网络图定义：有向图$G = (V, E)$，$distance(i,j)$表示i到j的最短路径长度如果存在的话，否则$distance(i,j)=\infty$
- $out-nbrs_i$代表图中的边从i指向这些节点
- $in-nbrs_i$代表图中的边从这些节点指向i

逻辑进程

定义：$V$代表分布式节点，即逻辑进程
包含的组件
- $state_i$：状态集合（并不是一定是有限状态）
- $start_i$：$state_i$的子集，开始状态或初始状态
- $msgs_i$：发送的消息，根据当前的状态生成消息发送给$i$直接指向的节点
- $trans_i$：收到的消息，状态转换方法收集收到的消息，然后进程转移到新状态

进程执行

消息生成：利用消息生成方法根据当前状态生成消息发送给所有$out-nbrs_i$
状态转换：利用状态转换方法收集消息根据当前状态获得新状态

故障类型

进程故障：节点停止故障、拜占庭故障（进程可以任意生成下一个状态和消息而不遵守进程消息生成和状态转换规则）
通信故障：链路故障(网络故障)

复杂度

用于分析分布式算法的效率

时间复杂度：进程生产所有输出或进程停止时已运行的轮数
通信复杂度：非空消息发送的次数

同步环网络Leader选举

同步环Leader选举的作用，首先假设一个同步环网络中有一个令牌，拿到令牌的进程可以执行，但是如果令牌丢失，那必须重新生成一个，生成这个令牌的过程就类似Leader选举过程。同步环网络结构如下图所示，下面将开始介绍同步环网络的Leader选举算法

LCR选举算法

算法来源：LeLann，Chang，Roberts三人提出的
算法思想：利用进程$uid$的唯一性，通过传递进程的$uid$来和各个进程比较，最终网络中最大的$uid$会流转一圈回到最初进程，因此最初进程就是Leader
前提假设
1. 每个进程有唯一的uid，下文称为$u$，最大$uid$的进程会被选举为leader
2. 各个进程组成一个环状网络的图$G$，结构如上，各个进程只能和相邻的进程通信
3. 单向网络，不依赖是否知道图的$G$的大小
进程维护状态
1. $uid$
2. $send$：一个$uid$或者$null$，初始为进程自己的uid，或者接受到的比自己大的$uid$
3. $status$：状态，值为$\{unknown, leader\}$，初始为$unknown$

算法描述

进程消息生成方法

如果send不为null，发送send的值给$process_{i+1}$

进程状态转换方法

send := null
if the income message is v ,a uid, then
	case
		v > u then send := v
		v = u then status := leader
		v < u then do nothing
	endcase

算法图解
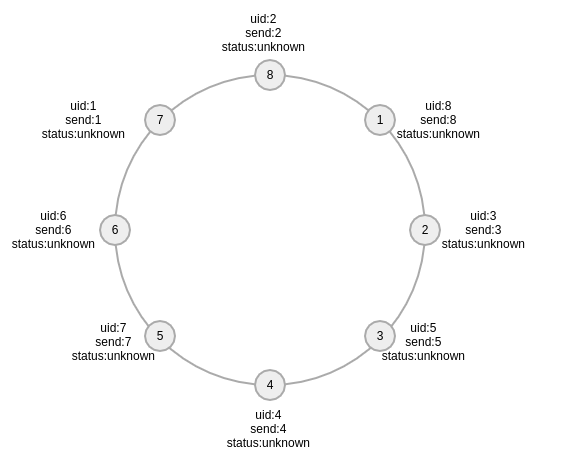
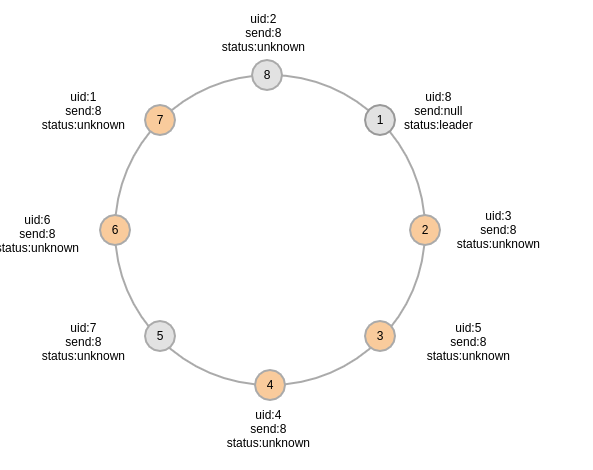
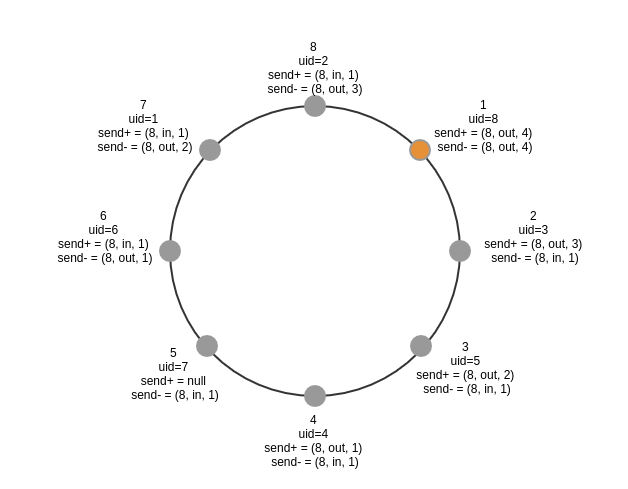
1. 初始状态，所有进程初始$send$都是自己的$uid$，$status$都是$unknown$
2. 第一轮之后的各进程状态，2,4,6号进程更新了自己的$send$状态
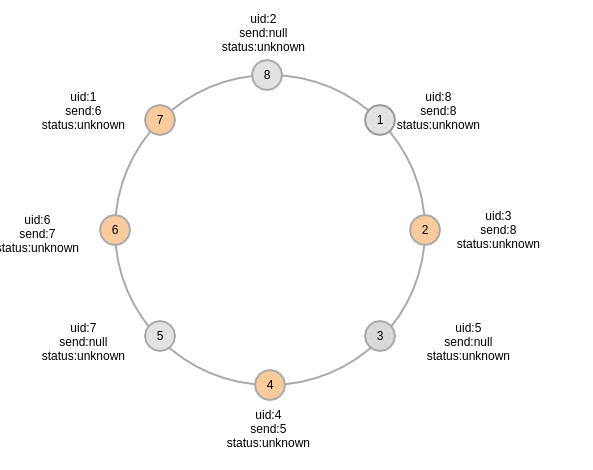
3. 第二轮之后，3,7号节点分别更新了状态
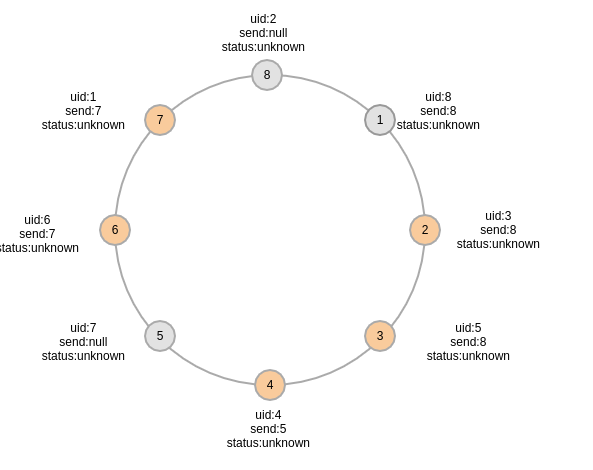
4. 第八轮之后，所有的节点$send$状态都更新了最大的$uid$，并且1号节点成为leader，此时选举并没有结束，除了1号节点，其他节点并不知道已经选举出leader
选举算法终止：上述过程经过8轮的通信已经选出1号节点为leader，但是此时其他节点并不知道选举过程已经完成，因为还需要8轮的通信将选举结果通报给各个节点
复杂度分析
- 时间复杂度：$O(n)$，终止选举过程算法版本时间复杂度为$O(2n)$
- 通信复杂度：$O(n^2)$，算法的通信复杂度很高

HS算法

算法来源：Hirschberg, Sinclair提出的一个最坏通信复杂度$O \log n$
算法思想：LCR算法通信复杂度为$O(n^2)$，当网络规模大时，通信开销太大。HS算法通过$l^2$扩大进程探索范围，然后分别在顺时针和逆时针方向传递$uid$并且比较，如果$uid$大于范围内的其他进程$uid$时继续传递，如果传递到探索边界时，回传$uid$，当最初发送进程收到自己发送的$uid$时，进入下一阶段$l+1$，因为在$l^2$范围内只有一个节点可以进入下一节点，其他进程不再发送探测信息，减少了通信开销
前提假设
- 和LCR不同，网络是双向网络
- 环大小未知
- 每个进程有唯一的uid，下文称为$u$，最大$uid$的进程会被选举为leader
进程维护状态
- $M$：$(uid,flag,hop-count)$，flag取值范围$(in,out)$，out代表是从i节点发出的，in代表是返回的消息
- $u$：$UID$
- $send+$：M数据结构，代表需要往顺时针方向发送的消息，初始化为$(uid,out,1)$
- $send-$：M数据结构，代表需要往逆时针方向发送的消息，初始化为$(uid,out,1)$
- $status$：取值集合$\{unknown,leader\}$，初始化为$unknown$
- $phase$：阶段初始化为0，每个阶段左右传递的距离为$2^{phase}$，因此最大值为$1+\log(n)$，包括阶段0

算法描述

消息生成算法
- 发送$send+$到$process_{i+1}$
- 发送$send-$到$process_{i-1}$

状态转换算法

send+:=null
send-:=null
if message from i-1 is (v, out, h) then
	case:
		v > u and h > 1: send+ := (v, out, h-1)
		v > u and h = 1: send- := (v, in, 1)
		v = u:  status := leader
	caseend
if message from i+1 is (v, out, h) then
	case:
		v > u and h > 1: send- := (v, out, h-1)
		v > u and h = 1: send+ := (v, in, 1)
		v = u:  status := leader
	caseend
if message from i-1 is (v, in, 1) and v != u then
	send+ := (v, in, 1)
if message from i+1 is (v, in, 1) and v!=u then
	send-:= (v, in, 1)
if message from i-1 and i+1 are both (u, in, 1) then
	phase := phase + 1
	send+ := (u, out, 2^phase)
	send- := (u, out, 2^phase)

说明

当h>1时，说明还在往外传($out$)，h=1时，说明是要回传($in$)
当$out$消息携带的$v=uid$时，那么说明当前进程的$uid$流转一圈后回到自己，说明没有比自己更大的$uid$，因此自己是网络的leader
当顺时针和逆时针方向的回传信息都回来时，说明在当前阶段的消息传递范围内没有比自己大的进程$uid$，其他进程都不会进入下一阶段

算法图解
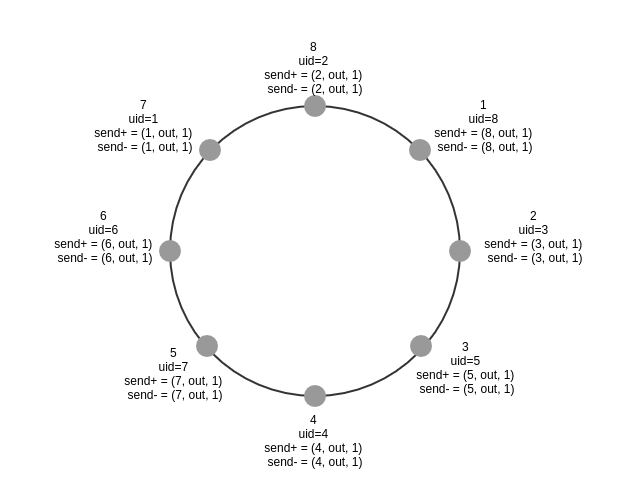
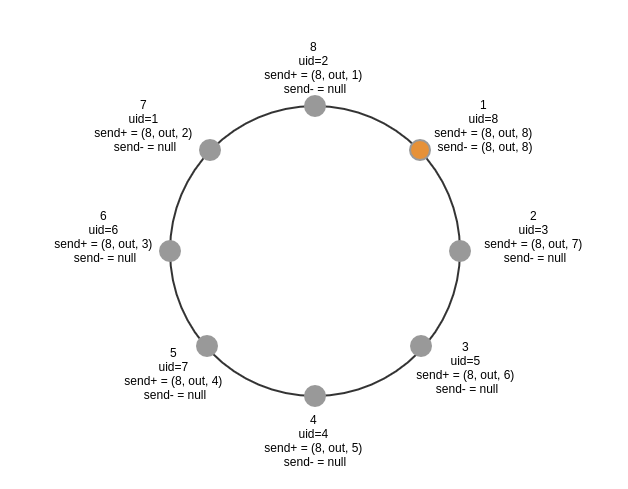
- 初始阶段
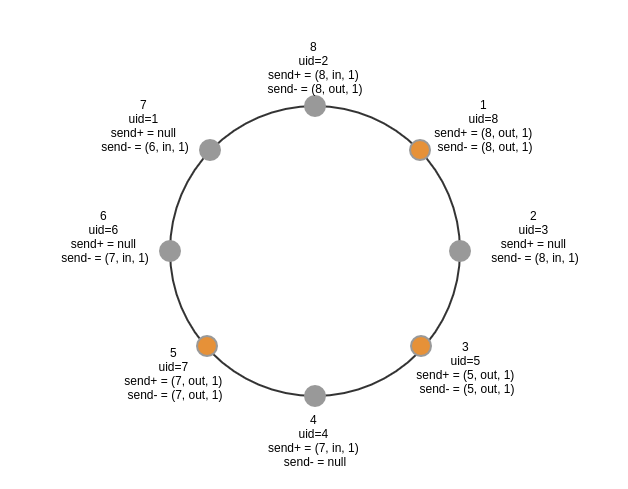
- phase 0阶段，顺时针、逆时针传递一个节点，示意图如下，因此最终完成phase 0的只有1、3、5节点
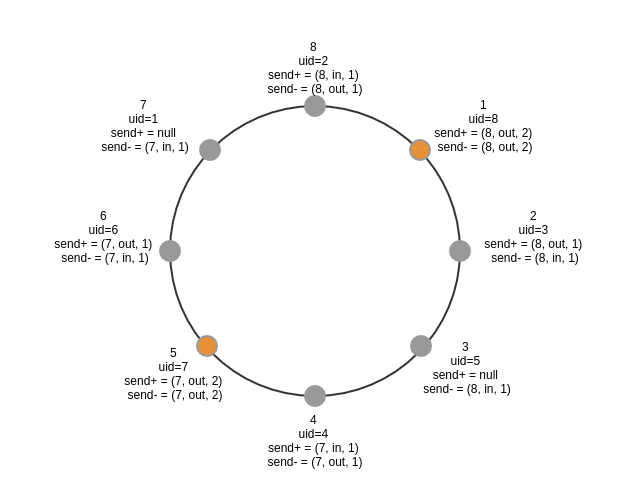
- phase 1阶段，传递两个节点，示意图如下，最终完成phase 1阶段的节点为1、5节点
- phase 2阶段，传递4个节点
- phase 3，最终阶段，传递8个节点，传回了自己，只画了顺时针示意图，这个阶段不再会有in标记的节点，因为不需要回传了
复杂度分析
- 通信复杂度
  1. 在phase=0阶段，总共需要发送4n条消息，每个节点会顺时针和逆时针方向发送消息并且收到回复消息
  2. 假设$l \gt 0$，因此在$l-1$阶段收到了最终的回复，所以节点i的uid为$2^{l-1}$范围内的最大值，那么有多少个节点会进入下一阶段呢？可以计算最多$\frac{n}{2^{l-1}+1}$
  3. 计算$l$阶段会发送多少条消息，$4(2^l \cdot (\frac{n}{2^{l-1}+1})) \le 8n$
  4. 上边提到过，$phase$最大为$1+\log(n)$，因此选出leader最大消息数$8n(1+\log(n))$，因此HS算法最坏通信复杂度为$O(n\log(n))$
- 时间复杂度
  1. 每个阶段时间$2 \cdot 2^l = 2^{l+1}$
  2. 最后一个阶段时间为n
  3. 倒数第二个阶段为$2 \cdot 2^{\log(n)-1}$
  4. 因此消耗的时间总数不超过$2 \cdot 2^{\log(n)}$，如果n为2的幂次，那么时间最多为3n或者5n，所以时间复杂度为$O(n)$

时间片算法(TimeSlice)

前边两种算法是基于比较的算法，基于比较的算法通信复杂度的下界是$O(n \log(n))$，基于时间片的算法是非比较的算法

前提假设
1. 同步网络环大小已知
2. 单向通信
算法思想：选举最小的UID进程，算法的核心思想是以一个时间片为一阶段，时间片一到，便升为另一个阶段，每个阶段会生成一个以阶段号为v的令牌在环中流转n次，所有收到消息节点都会停止选举，而如果一个进程uid为v，而在v-1阶段前都没有收到非空消息，则它选举自己为leader并发出宣告，其他进程收到消息后都停止选举
复杂度分析
- 通信复杂度：总数为$n$
- 时间复杂度：$O(n*u_{min})$，由于其时间复杂度几乎无上界，导致它的实用性很差，只能用于那些规模很小，uid很小的网络

通用网络中Leader选举

上边介绍了同步网络环的选举算法，下边将介绍通用网络的选举算法

FloodMax算法

概念
- $diam$：图中任意两个节点最远距离
前提假设
1. 任意的有向强联通图
2. 进程有唯一的$uid$
3. 图的大小已知
算法思想：每个进程发送自己当前接收到的的$max-uid$给相邻的进程，经过$diam$轮数后，如果收到的最大$uid$等于进程的$uid$，那么该进程就是leader
算法维护状态
1. $u$：uid初始化为uid
2. $max-uid$：当前进程接收到的uid，初始化为进程uid
3. $status$：取值范围$\{unknown,leader,non-leader\}$，初始化为$unknown$
4. $rounds$：一个整数，初始化为0

算法描述

消息生成算法

1 2	if rounds < diam then send max-uid to all j(out-nbrs)

状态转换算法

rounds := rounds + 1
let U be the set of uids that arrive from processes in in-nbrs
max-uid := max(max-uid, U)
if rounds = diam then
	if max-uid = u then status := leader
	else status := non-leader

算法图解
- 初始状态，根据图，我们知道图的直接$diam$为6，因此需要运行6轮
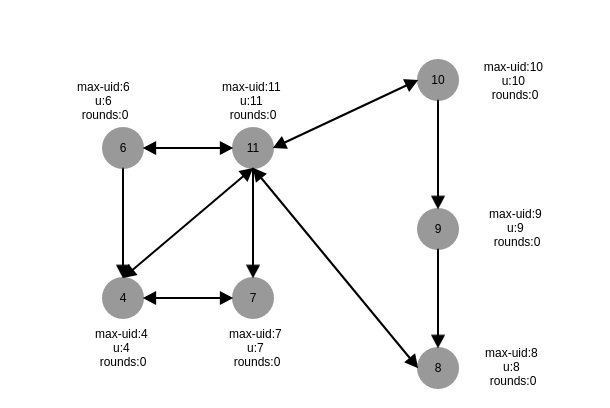
- 第一轮
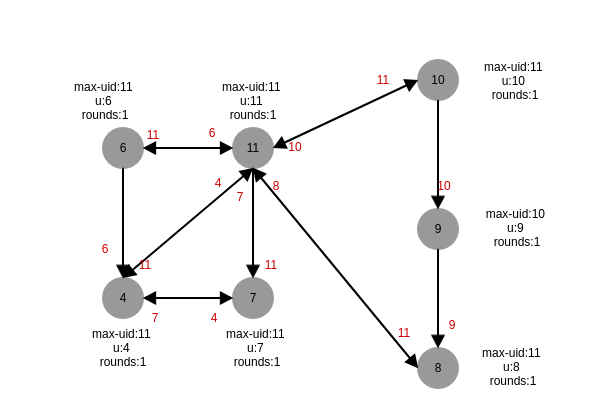
- 第二轮
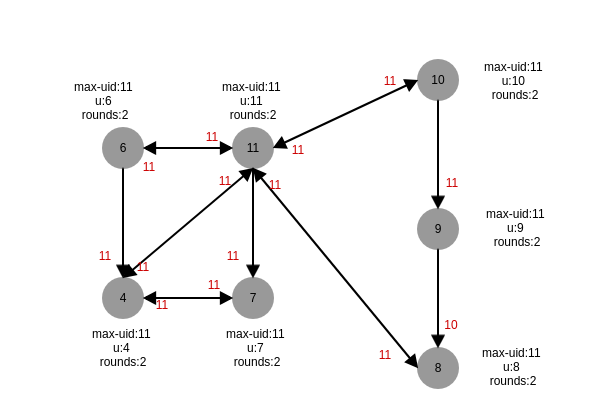
- 第六轮，最终uid为11的进程选举为leader
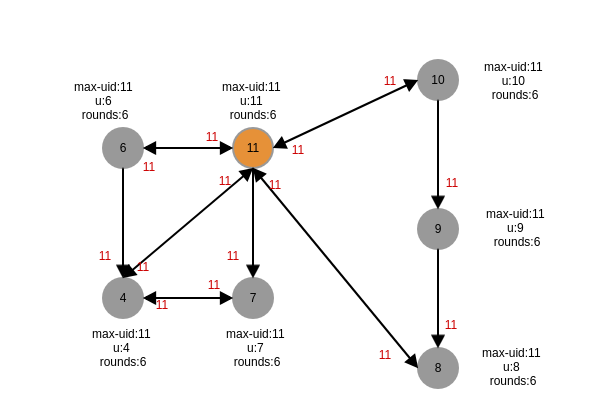
复杂度分析
- 时间复杂度：选出leader时，一共发送了$diam$轮，因此时间复杂度为$O(diam)$
- 通信复杂度：总共发送的消息数为$diam \cdot|E|$，$|E|$代表各节点的$out-nbrs$数

OptFloodMax算法

OptFloodMax是FloodMax的优化，目的是为了减少通信次数

进程维护状态
- FloodMax算法需要维护的状态
- $new-info$：$status$附加的属性，boolean类型，初始化为true，只有为true时才会转发消息

算法描述

消息生成算法

1 2	if rounds < diam and new-info = true then send max-uid to all j(out-nbrs)

状态转换算法

rounds := rounds + 1
if max(U) > max-uid then new-info = true else new-info = false
max-uid := max(max-uid, U)
if rounds = diam then
	if max-uid = u then status := leader
	else status := non-leader

总结

本文简单介绍了同步网络选举算法，之后的文章会介绍同步网络的其他算法