分布式系统-3-同步网络算法

引言

上一篇文章讲了同步网络中的leader选举算法。考虑一个问题，当网络中有消息需要广播时，如果在网络中以最快的速度完成广播？或者如何计算图的直径？接下来就会一步一步解决这些问题

将在这篇文章中讲述分布式同步网络中广度优先搜索、最短路径和最小生成数算法。

广度优先搜索

利用广度优先搜索来构造方便用于广播通信的树，BFS树最小化最大通信时间

SynchBFS算法

前提假设
1. 假设进程有uid
2. 不知道网络大小和直径
3. 给定初始root $i_0$

进程维护状态
1. $parent$：记录进程的父节点是谁
2. $marked$：记录是否被标记
算法流程
- 选择一个节点作为初始节点，定为$i_0$，设置为已标记，$i_0$发送一条search消息到节点$i$的$out-nbrs$
- 对于任意一个节点，如果节点还未被标记，并且收到search消息，则它将自己标记，并且将发送search消息的节点设置为它的parent，然后发送search消息到它的$out-nbrs$
算法图解
- 初始化选择4(可以随意选择)为root节点$i_0$
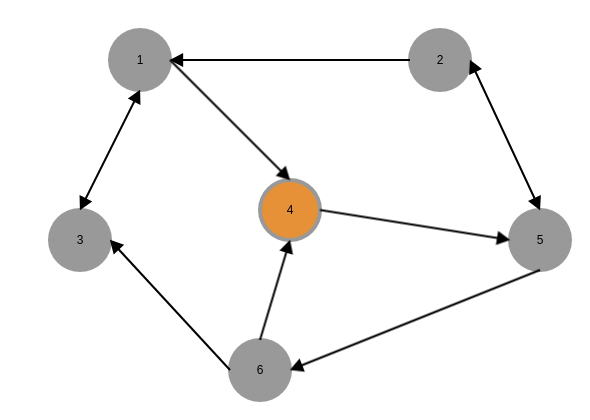
- 第一轮search消息，4只有一个$out-nbrs$，所以只有一条消息，5被标记，其parent节点为4，红色箭头代表search消息
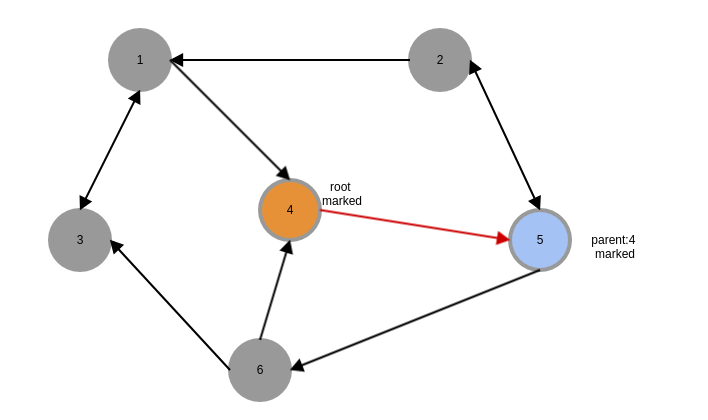
- 第二轮search消息,5有两个$out-nbrs$
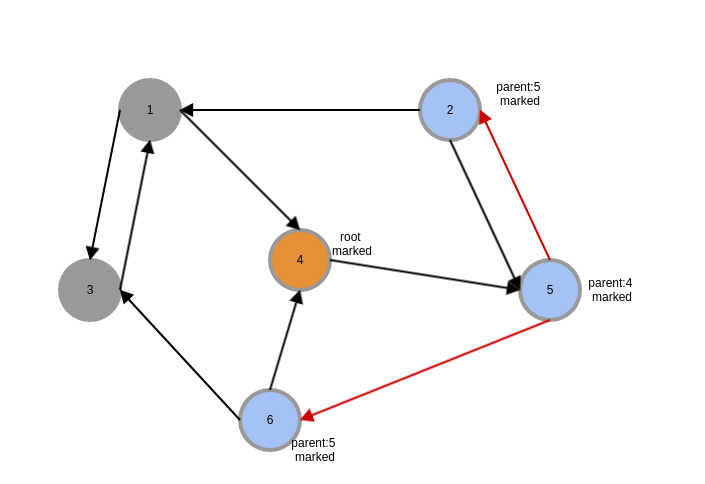
- 第三轮，因为是分布式系统，所以进程2和进程6是同时进行的
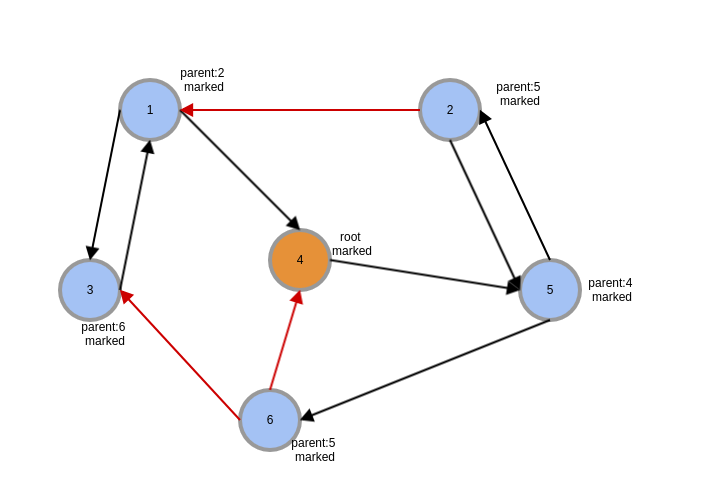
复杂度分析
- 时间复杂度：最多为daim轮，为图的直径，实际上可能更小，是$i_0$到它最远的节点
- 通信复杂度：通信复杂度：图的边数，$|E|$
如何确定child节点：双向网络中非常容易，child发送一条消息给parent。在单向网络中，需要间接节点将消息传递给它的parent节点，因此可以用SynchBFS算法实现这个过程，如果每一轮中一条链路只能发送一条消息，那这些消息可以合并成一条消息
- 复杂度分析
  - 双向通信网络
    1. 时间复杂度：$O(diam)$
    2. 通信复杂度：$O(|E|)$，因为child可以直接发送消息给parent，因此总消息数为$2\cdot|E|$
  - 单向通信网络
    1. 时间复杂度：$O(diam)$，因为额外的消息可以并行发送
    2. 通信复杂度：$O(diam\cdot|E|)$，因为需要发送额外消息，因此每一轮中每条边都可能会发送消息，总共有$diam$轮，所以总消息最多为$diam\cdot|E|$
SynchBFS算法终止
- 核心思想：当消息传递到叶子节点时，叶子节点标记自己后，发送消息让parent知道其已经完成，当parent收到所有其子节点的确认完成消息后，parent发送消息给它的parent，循环这个过程直到确认消息到达root节点$i_0$
- 复杂度分析
  - 双向通信网络
    1. 时间复杂度：$O(diam)$，因为叶子节点返回确认完成消息是并行执行并且可以直接发送给parent，因此，时间最多为$2\cdot diam$
    2. 通信复杂度：$O(|E|)$
  - 单向通信网络
    1. 时间复杂度：$O(diam^2)$，因为在发送确认消息时，每一级parent都是执行一次SynchBFS算法，每一层级的节点不能并行执行，因为不能确定，该级的parent是否收到了所有child的确认消息，因child是通过间接的节点传递消息，因此可能绕了一个diam的路径，最多有diam个层级，因此时间复杂度为$O(diam^2)$
    2. 通信复杂度：$O(diam^2\cdot|E|)$，和确认child节点类似，虽然每个层级的节点确认完成消息不能并行执行，但是不同节点的确认可以并行执行，因此每一轮最多有|E|消息，每一层级的确认消息最多需要$diam$轮，因此每一层级的确认需要消息最多为$diam\cdot|E|$，最多需要$diam$轮才能完成到$root$的确认，因此通信复杂度为$O(diam^2\cdot|E|)$
算法应用
- 广播：一条消息的广播可以建立在BFS tree上，利用SynchBFS构造的一颗每一个非叶子节点都包含其子节点的BFS树，因此广播一条消息只需从root一直向前传播，时间复杂度为$O(diam)$，通信复杂度为$O(n)$
- 全局计算：比如网络中所有节点求和，利用BFS tree从叶子节点开始，发送一个值给parent节点，非叶子节点等到汇集了所有子节点的输入，sum后发送给它的parent节点，直到root节点。如果在双向网络中，时间复杂度为$O(diam)$，通信复杂度为$O(n)$
- leader选举：所有节点初始并行发送消息进行选举，利用最大uid构造树，在双向网络中，时间复杂度为$O(diam)$，通信复杂度为$O(diam\cdot|E|)$
- 计算图的直径(FloodMax需要用到)：所有节点并行发送消息执行SynchBFS算法，每个进程利用$max-dist_i$来构建树，得每个节点得到一个最大值，然后在第二轮中，整个网络利用SynchBFS求出最大值。如果是双向网络，时间复杂度$O(n)$，通信复杂度$O(diam\cdot|E|)$

最短路径

SynchBFS解决了未带权边的搜索，但是实际环境中，有很多场景并不是这样简单的，通常节点间通信都是有开销的，这个开销我们可以抽象为权重，比如通信的延迟，或者通信的带宽等，接下来将介绍带权网络的算法

BellmanFord算法

前提假设
1. 有向网络
2. 有向边关联了一个权重
3. 每个节点知道连接边的权重
4. 每个节点知道网络的大小
进程维护状态
1. $dist$：从$i_0$到该节点的最短距离，$i_0$初始化为0，其他初始化为$\infin$
2. $parent$：最短路径的父节点，初始化为$undefine$
3. $round$：轮数，当$round$为n-1时结束

算法描述

消息生成算法

1 2	if round <= n-1 then send (dist, uid) to out-nbrs

进程状态转换算法，每一轮收到消息M的$(dist,uid)$,收到M集合U

if round <= n-1 then 
min := min(U.dist)
if min+weight < dist then 
	dist := min.dist+weight
	parent := min.uid 
round := round+1;

算法图解
- 初始状态
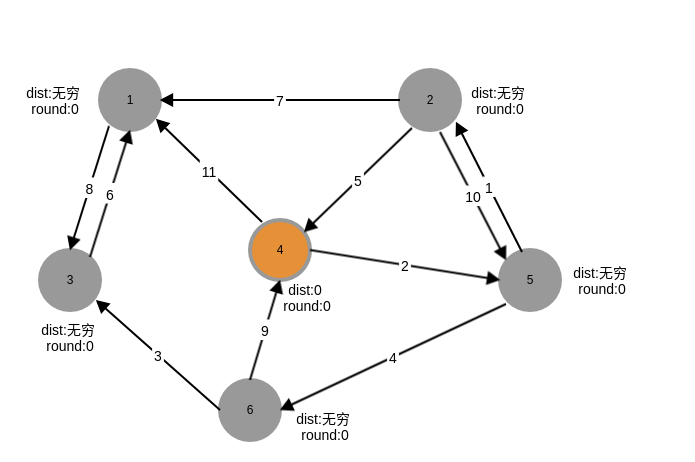
- 第一轮，红色的线表示最短路径
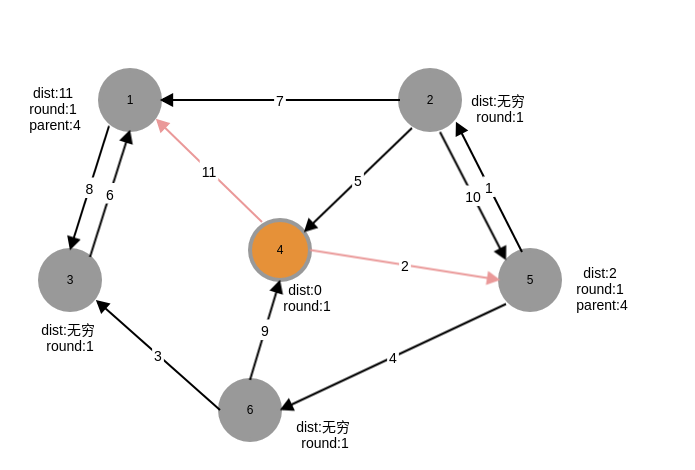
- 第二轮
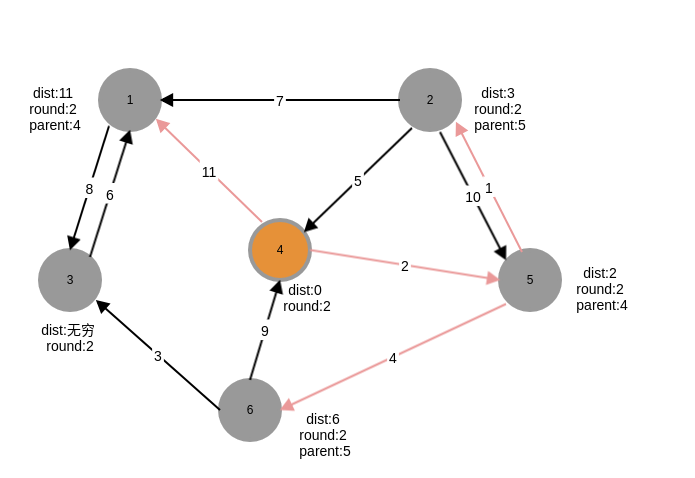
- 第三轮，可以看到节点1，最短路径已经有更小的值，其父节点也换成了2，直到$n-1$也就是round=5时，算法结束
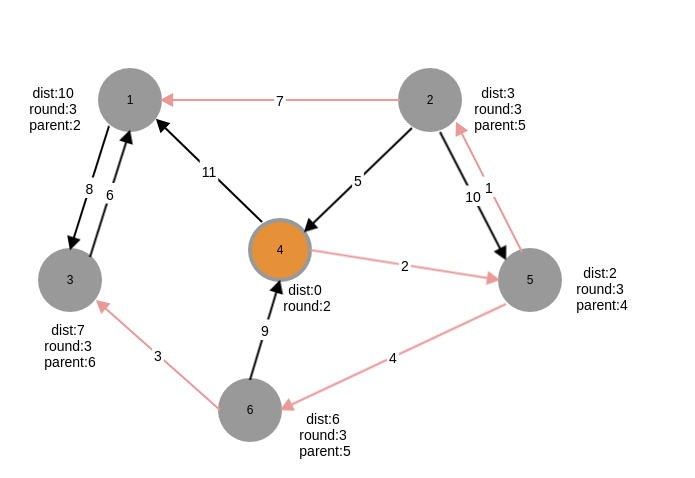
复杂度分析
- 时间复杂度为$n-1$
- 通信复杂度$(n-1)\cdot|E|$

最小生成树

SynchGHS算法

前提假设
1. 带权无向图
2. 节点有$uid$
3. 图大小已知
进程维护状态
1. leader：记录component(一个子树结构)的leader的$uid$，
2. k：level，每个level至少有$2^k$个节点
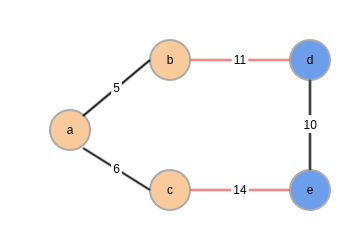
MWOE(最小权重出边)：指连接两个component的最小权重的边，一个简单的图说明，橙色和蓝色分别是两个不同的component，两条红色的边都是两个component的连接边，权重11的边就是要找的MWOE
算法原理
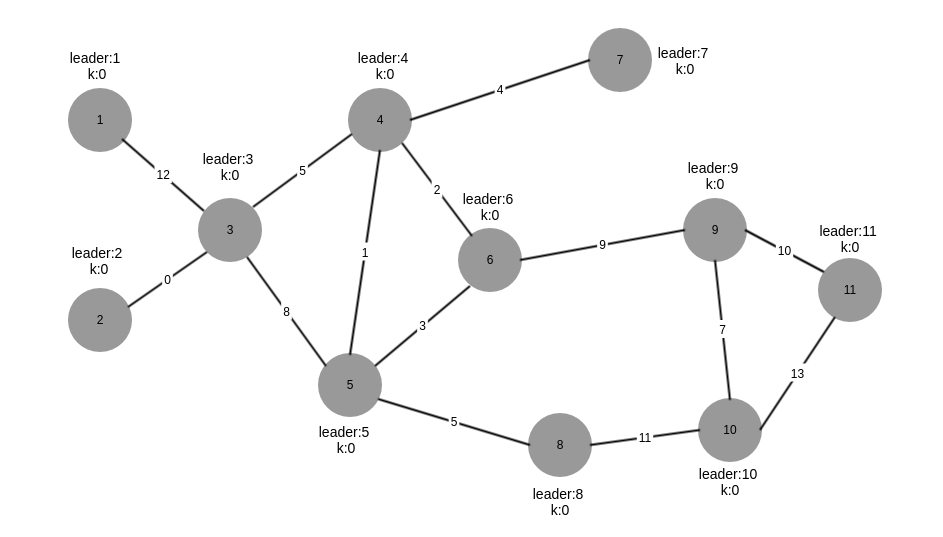
- 初始时，所有单个节点是一个component，每个节点的leader即是自己，每个component找出最小权重的出边MWOE，当一个component有多个节点时，会采用广播让各个节点找到MWOE，然后发送测试消息，看另一端的节点是否属于同一component，然后汇集MWOE到leader，leader得到整个component的MWOE。比如1只有一个边12，而3和2正好有同一条最小边0，所有这些操作都是并行执行的。
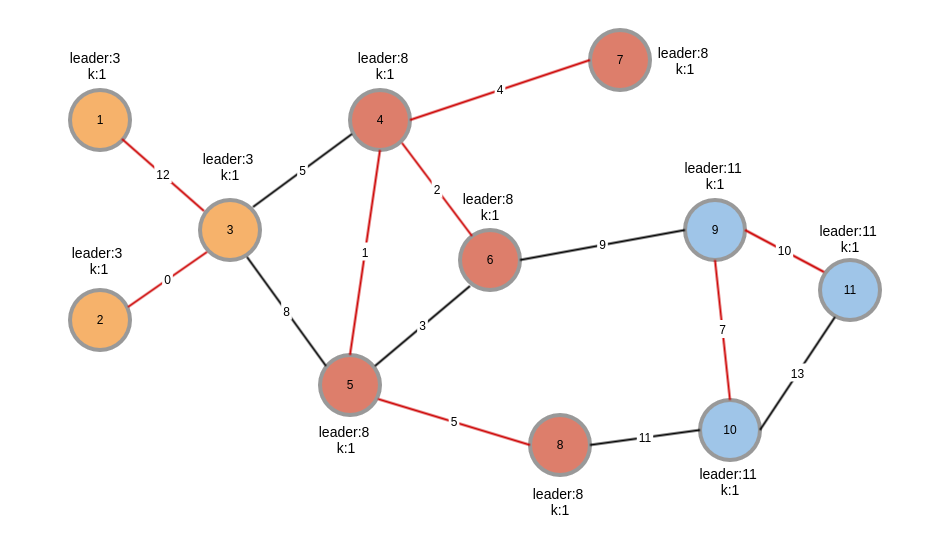
- 合并，leader通知component的MWOE的节点进行连接操作，节点将边加入树并通知端点节点进行同样的操作，然后节点uid大的端点节点利用树广播leader信息，宣布自己是leader，当有多个component合并成一个时，因为多个节点会广播leader信息，因此最终，整个component都会得到最大uid的leader信息，新component拥有了新的标识.（这里我的理解是可以直接使用当前component的Leader，但是书中描述的是用MWOE的端点uid大的作为新的leader）
- 算法终止，当所有的节点都联成一个图后，leader通知各节点寻找MWOE时，将没有MWOE了，因此leader通知各节点算法结束
复杂度分析
- 时间复杂度：因为每一级合并至少有两个component合并，因此最多需要$\log(n)$级可以完成MST构建，每一级需要的时间为$O(n)$，因此时间复杂度为$O(n\cdot\log(n))$
- 通信复杂度：每一级，leader需要发送消息通知树的各个节点寻找MWOE，图中共有n个节点，找到之后还要汇集结果，因此消息数为$2\cdot n$，因此通信复杂度为$O(n)$，各个节点探测MWOE时，可能每条边都要探测，因此还需要额外的$|E|$通信消息，因此整体的通信复杂度为$O((n + |E|)\log(n))$
优化：在测试边时，如果是一条内部边也就是端点都是同一component，那么就标记为”rejected”，当探测时，如果一条边是rejected，那就不需要发送探测消息，因此探测通信总共只需要执行$|E|$次，因此通信复杂度为$O(n\log(n) + |E|)$

最大独立集(MIS)

定义：假设有无向图$G=(V,E)$,其中$I \subseteq V$是图的独立集，当且仅当$i,j \in I (i,j) \notin E$，通俗的讲就是最大独立集中的任意两个节点之间没有边相连，因此MIS不是唯一的。$I$是最大独立集当任意$I^$包含$I$且$I^$不是独立集
前提假设
1. 知道图的大小$n$
2. 不假设节点有$uid$
算法核心思想：每次选择独立集$I^$，然后将$I^$执行操作$I := I\bigcup I^$，然后从图$G$中删除$I^$的邻居，直到$G$为空，因此问题的关键是求$I^`$

LubyMIS算法

利用随机化算法求$I^{\prime}$

算法思想：每个节点$i$随机选择一个随机数$val_i$(范围$1 \le val_i \le 4^n$)，然后相邻节点之间发送消息$val_i$的最大为$winner$，$winner$会通知它的相邻节点为$loser$。$loser$会被从图$G$中移除
进程维护状态
1. $round$：取值{1,2,3}，初始值1
2. $val$：取值$\{1 \le val \le 4^n\}$，初始任意值
3. $awake$：boolean值，初始值true
4. $rem-nbrs$：剩余没有选择的邻接节点，初始化为图的所有邻接节点
5. $status$：$\{unknown, winner, loser\}$，初始值$unknown$

算法描述

随机数生成

1	if awake and round = 1 then val := random

消息生成算法

if awake then
case
	round = 1:
		send val to all nodes in rem-nbrs
	round = 2:
		if status = winner then
			send winner to all nodes in rem-nbrs
	round = 3:
		if status = loser then
			send winner to all nodes in rem-nbrs
endcase

状态转换算法

if awake then
case
	round = 1:
		if val > v in all incoming values v then status := winner
	round = 2:
		if a winner message arrives then status := loser
	round = 3:
		if status in {winner,loser} then awake:=false
			rem-nbrs := rem-nbrs - {j: a loser message from j}
endcase
round := (round+1) mod 3

算法图解
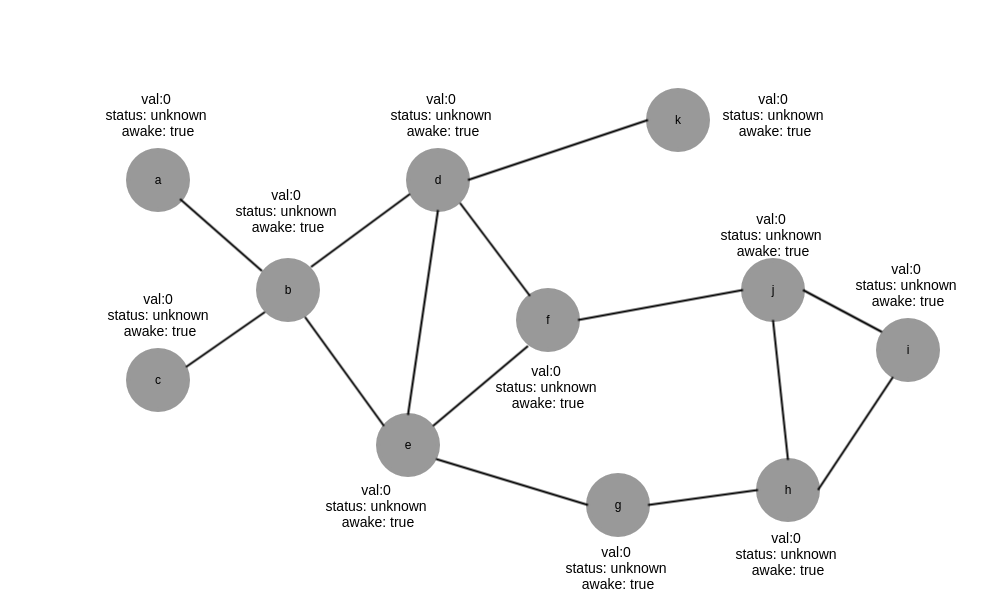
- 初始状态，注意LubyMIS算法并不需要$uid$，图中的字母编号仅仅是为了方便图的说明，不是$uid$，初始时所有节点$awake$都是true，状态都是$unknown$，$val$任意值，统一初始化为0
- 第一阶段结果示意图，每个阶段有三轮，这里只展示结果，橙色节点代表$winner$节点，蓝色节点代表$loser$节点，注意观察，不管蓝色节点还是橙色节点$awake$都是false，也就是它们已经结束不会再参与算法运行，可以看到已经只有a、k节点会进入下一阶段
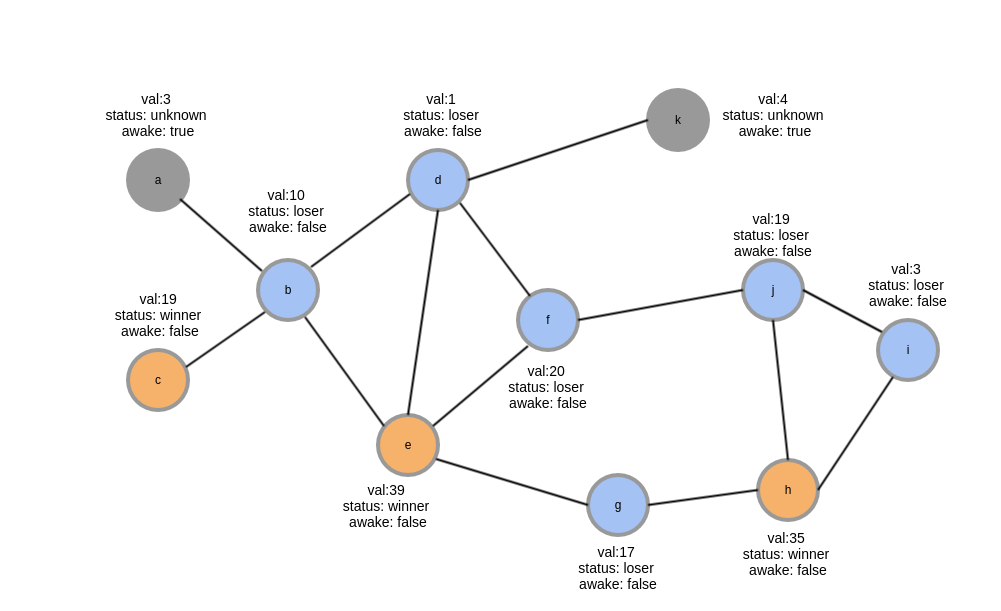
- 第二阶段结果示意图，经过第二轮，重新生成随机数，所有节点$awake$都是false，全部节点都已经运行结束，因此该图的最大独立集为$(a,c,e,h,k)$
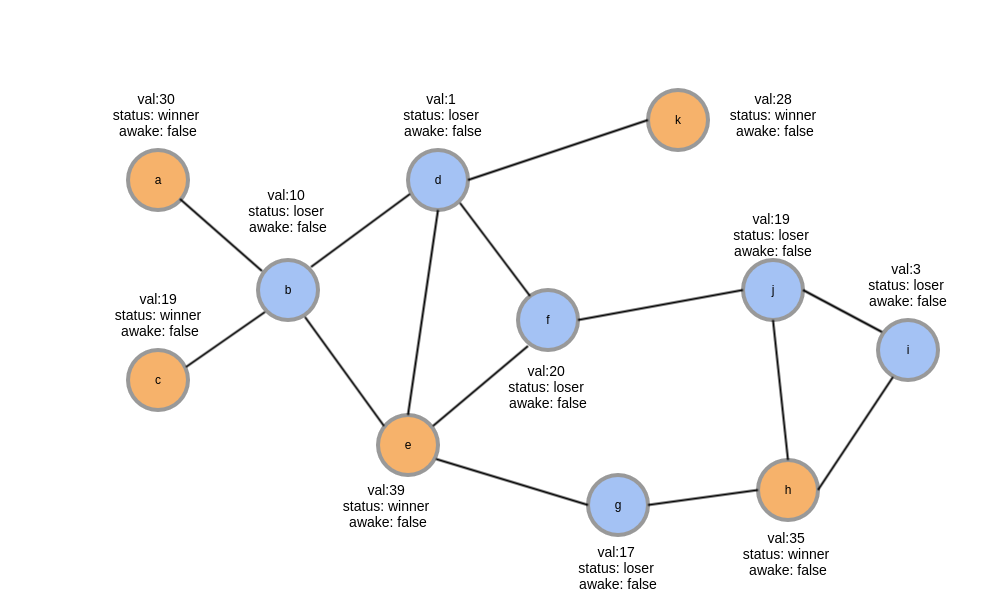
随机化算法作用：主要作用是打破对称性，是一个非常常用的小技巧，比如在解决活锁，在raft协议选举失败时为了避免所有节点同时发起选举，失败后都会随机等待一段时间后发起选举

总结

本文主要讲了分布式同步网络中的BFS、最短路径、MST问题，接下来的文章将简单介绍分布式同步网络另一个关键性问题，一致性问题