分布式系统-4-同步网络一致性算法

引言

上一篇文章讲了分布式同步网络算法中的BFS、最短路径、MST和MIS算法，这一篇文章将会将分布式系统中一个非常重要的问题-一致性。在单节点的环境中，一致性问题是比较容易解决的，像单节点的数据库，因为只有一个节点，也就不存在数据不一致的说法。

因为机器总会有概率出故障，如果仅仅是单节点应用，一旦机器发生故障，那么服务将不可用。为了提供高可用的应用，多节点部署应用成为一种解决方案，但是多节点部署应用也引发了一些问题，比如节点故障依然存在；并且因为多节点，导致节点间需要通信，因此系统存在通信故障，如果机器不是在自己机房内，可能要有Byzantine故障，这些问题都可能导致数据一致性问题。比如，在分布式数据库事务中，假设两个进程a，b需要通信来达成是一致（提交或者回滚），因为通信故障，a收到b的提交请求，但是b没有收到a的请求，此时a可能会提交，而b可能回滚，那么就出现数据不一致。

接下来的文章的结构是，第一部分是介绍在分布式同步网络中，如何在通信故障下解决一致性问题；第二部分介绍，如何在节点停止故障下解决一致性问题；第三部分介绍，如何在节点出现Byzantine故障下解决一致性问题。

通信故障下一致性

协同攻击问题

定义：几个将军协同攻击问题，所有将军通过信使互相传递消息，经过图的直径轮后，消息会传递给各个将军，最后决议是否发起攻击，但是如果有消息丢失，那么将军无法达成一致。在计算机中，比如分布式数据库事务

决议满足的条件
1. 一致性：没有两个进程决议不同的值
2. 有效性：如果所有进程初始值为0，那么决议值只能是唯一的0；如果所有进程的初始值为1，那么决议值只能是唯一的1
3. 终止性：所有进程最终为做出决议

协同攻击问题-随机化版

定义：对消息丢失做一定概率性假设，然后必须允许一定概率违反一致性和有效性
前提假设
1. 每个进程有确定的起始状态
2. 知协议在固定的$r \ge 1$轮终止，在$r$轮后，每个进程节点需要输出它的决议
3. 消息的丢失不是随机发生，而是由“对手”决定的
通信模式
- $(i,j,k)$中$(i,j)$是图的一条边，$k \ge 1$，代表在k轮的从i发给j的消息
- 定义通信模式$\gamma$是good，一系列的$(i,j,k)$消息投递成功的
- 对于任意的对手B不一致的概率为，$Pr^B\{some process decides 0 and some process decides 1\} \le \epsilon$
“对手”的作用
- 为图中每个节点分配input值
- 定义一个good的通信模式

RandomAttack算法

前提假设：为简单起见，假设图是n节点的完全图(完全图是指图中任意两个节点都有直接边连接)
定义通信模式
- 通信模式$\gamma$这里指的是消息的偏序关系，$(i,k)$代表i节点的k时刻，有如下关系
  1. 对于所有的$1 \le i \le n$和所有的$0 \le k \le k^{\prime}$满足$(i,k) \le_{\gamma} (i,k^{\prime})$
  2. 如果$(i, j, k) \in \gamma$，则有$(i, k-1) \le_{\gamma} (j, k)$
  3. 传递性，如果$(i, k) \le_{\gamma} (i^{\prime}, k^{\prime})$并且$(i^{\prime}, k^{\prime}) \le_{\gamma} (i^{\prime \prime}, k^{\prime \prime})$则有$(i,k) \le_{\gamma} (i^{\prime \prime}, k^{\prime \prime})$
- 定义$level$，用$level_{\gamma}(i,k)$表示进程$i$在$1 \le k \le r$的值，值的规则如下
  1. 如果$k = 0$，那么$level_{\gamma}(i,k) = 0$
  2. 如果$k>0$并且有$j \neq i$使得$(j,0) >_{\gamma} (i, k)$，那么$level_{\gamma}(i,k)=0$
  3. 如果$k > 0$并且$j \neq i$使得$(j,0) \le_{\gamma} (i, k)$，对于所有的$j \neq i$用$l_j$表示$max(level_{\gamma}(j,k^{\prime}):(j,k^{\prime}) \le_{\gamma} (i, k))$，注意所有的$l_j$满足$0 \le l_j \le k-1$，那么$level_{\gamma}(i, k) = 1+min(l_j:j\neq i)$
- 一个简单的两个节点通信示意图
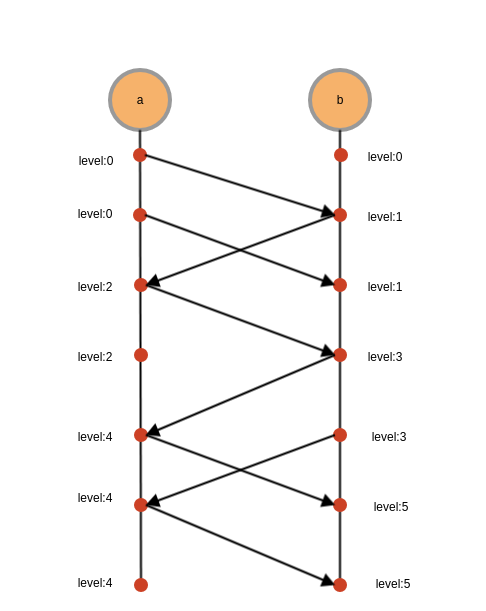
算法思想：算法思想：进程1随机生成一个$key$，$key$的范围为$[1,r]$，当算法运行到$r$轮时，所有进程i会判断如果$key \le l_i$并且所有的进程初始值$val$为1，那么它的$decision=1$，其他情况$decision=0$
进程维护状态
1. $rounds$:已运行的轮数，初始化为0
2. $decision$：最后的决议，取值$\{unknown,0,1\}$，初始化为$unknown$
3. $key \in [1, r] \bigcup undefined$，初始化为$undefined$
4. 对于所有的j，$1 \le j \le n$
  1. $val$：一个数组，$val_j \in \{0, 1, undefined\}$，初始化$val_i = i_{val}$，对于所有$j \neq i$，$val_j=undefined$
  2. $level$：一个数组，$level_j \in [-1,r]$，初始化$level_i = 0$，对于所有$j \neq i$，$val_j=-1$

算法描述

$key$的生成
1
if i=1 and rounds=1 then key := random

消息生成算法

1	send (L, V, key) to all process j, L是level向量，V是进程val向量

状态转换算法

rounds := rounds+1
let (Lj, Vj, kj) be the message from j, for each j from which a message arrives
if, for some j, kj != undefined then key := kj
for all j != i do
	if V(j) != undefined then val(j) := V(j)
	if L(j) > level(j) then level(j) := max(L(j))
level(i) := 1+min(level(j) : j!=i)
if rounds = r then 
	if key != undefined and level(i)>=key and val(j)=1 for all j then
		decision := 1
	else decision := 0

在第r轮对$key$分析，通过分析，我们可以得到在进行$r$轮通信之后，不一致的概率为$\frac{1}{r}$，因为key的取值范围为$[1, r]$
1. 如果对于所有进程$key \le min(l_j)$，那么所有$decision$是一致的，如果所有的val为1，那么$decision$为1，否则为0
2. 如果对于所有进程$key > max(l_j)$，那么所有$decision$也是一致的，为0
3. 如果对于所有进程$key = max(l_j)$，对于这种场景，便会出现不一致，因为有的进程$decision$可能为1，有的为0
不一致概率的下界分析：$\epsilon \ge \frac{1}{r+1}$

节点停止故障

本小结讲的是在节点停止故障下，如何保证分布式系统的一致性

前提假设
1. 假设网络是n节点的无向连通图
2. 各个进程有相同的input集V
3. 假设通信链路是可靠的
4. 假设网络中故障的节点数上限为$f$
决议满足的条件
1. 一致性：没有两个进程决议不同的值
2. 有效性：所有进程有相同的初始值$v \in V$，因此v是唯一的最终决议
3. 终止性：所有正常进程最终决议

FloodSet算法

算法思想：一个很简单的解决进程停止故障时一致性的算法，它的核心思想是每个进程重复的广播它见到的所有值。
前提假设
1. 满足上述的前提假设
2. 网络是完全图
进程维护状态
1. $rounds$：初始化为0
2. $decision$：范围$V \bigcup unknown$，初始化为$unknown$
3. $W$：$W \subseteq V$，初始化为进程$i$的初始值
算法描述
- 消息生成算法
  
  if $rounds \le f$ then send W to all processes
- 状态转换算法
  1. rounds := rounds+1
  2. let $X_j$ be the message from j,for each j from which message arrives
  3. $W:=W \bigcup (\bigcup_j X_j)$
  4. if rounds = f+1 then if $|W|=1$ then decision = v where $W=\{v\}$ else decision = $v_0$
复杂度分析
- 时间复杂度：$O(f+1)$
- 通信复杂度：$O((f+1)n^2)$
OptFloodSet算法
- 优化原理：为了减少通信，只有当进程发现新的不同值时才广播一轮消息，这样每个进程最多发送两轮消息，第一轮为第一次，第二轮为接收到不同的值
- 通信复杂度：通信数目最多为$2n^2$

指数信息收集算法(EIG)

EIG Tree介绍
- EIG Tree结构如下图，因为其收集的信息随着轮数的增加呈指数增长，因此得名指数信息收集
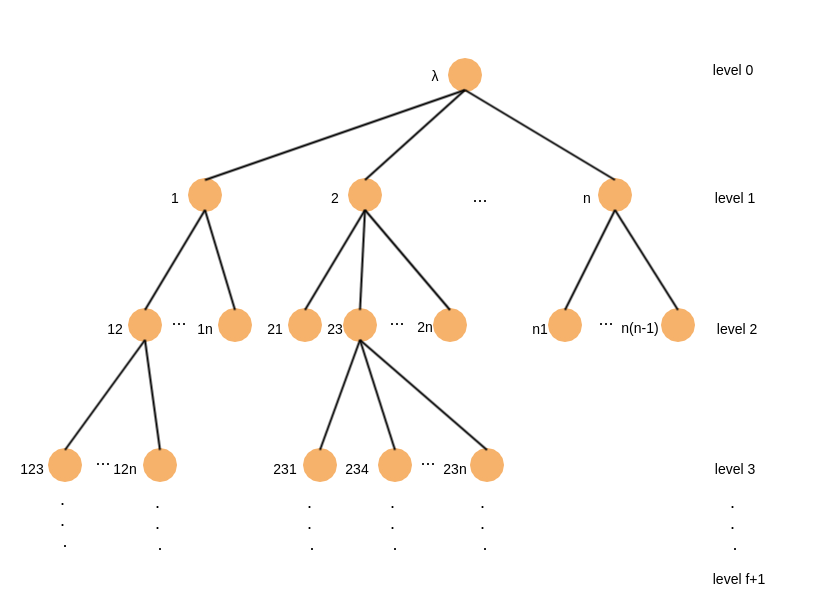
- EIG Tree解释
  1. level 0的$\lambda$代表进程i的初始值
  2. 为了统一处理，进程可以发送消息给自己
  3. 第k层的节点，含有$n-k$个子节点，如上图$level 0$含有n个子节点
  4. 节点代表的含义，如$level1$的各节点代表从各个进程发送给来的值，比如节点1代表从进程1发送过来的值；$level2$的值是由各进程发送$level1$的值，比如23代表从进程3发送的$level1$的2的值。一般性的，假设字符串123之类的表示为$i_1i_2…i_k$，代表从第i个进程发送$level k$的$i_1i_2…i_{k-1}$的值，依次类推。因此假设$i_1i_2…i_kj$，那么j的范围为$\{1,…,n\} - \{i_1,i_2…i_k\}$的集合
  5. 为什么是$n-k$呢？在$level1$时，接收来自各个进程的值包括自己进程，$level1$时，比如12，进程1发送来的值已经知道了，所以进程1不需要发送1的值，依次类推
EIG算法核心思想：在不同的轮中，把从不同通信链路中收集的值记录在特殊的数据结构中，其实本质就是间接的从其他进程那里获得目标进程的值，因为进程1可以在发送了值给进程2还没发送给进程3时挂了，那么在下一轮中进程3可以通过进程2得知进程1的值。和FloodSet算法比起来，似乎EIG算法开销大的多，但是EIG还可以用来解决Byzantine故障的一致性
EIG算法执行步骤
1. round=1
  1. 如果$v \in V$的值从j通过消息发送到i，那么设置$val(j)=v$
  2. 如果没有消息，那么设置$val(j)=null$
2. $2 \le round \le n-k$
  1. 如果$v \in V$从j通过消息发送的$val(x)$到i，那么i进程的$val(xj)=v$
  2. 如果没有消息从j发送$val(x)$到到i，那么i进程的$val(xj)=null$
3. 在$round = f+1$轮后，通过统计EIG Tree中的值，如果只有一个值，那么进程的决议就是这个值，如果有多余一个值，那么决议值为默认$v_0$
一个简单的例子，3个进程，假设$f=1$个进程故障，所以总共需要$f+1=2$轮
1. 初始状态
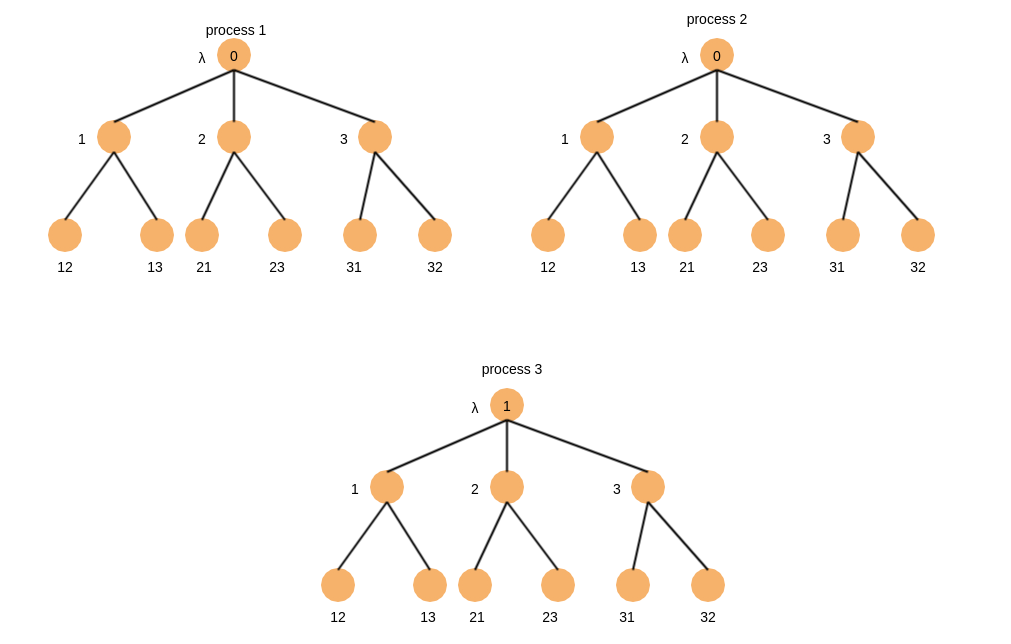
2. round=1，假设进程3发送消息给进程1后还没发消息给进程2时进程3宕机了，那么状态如下
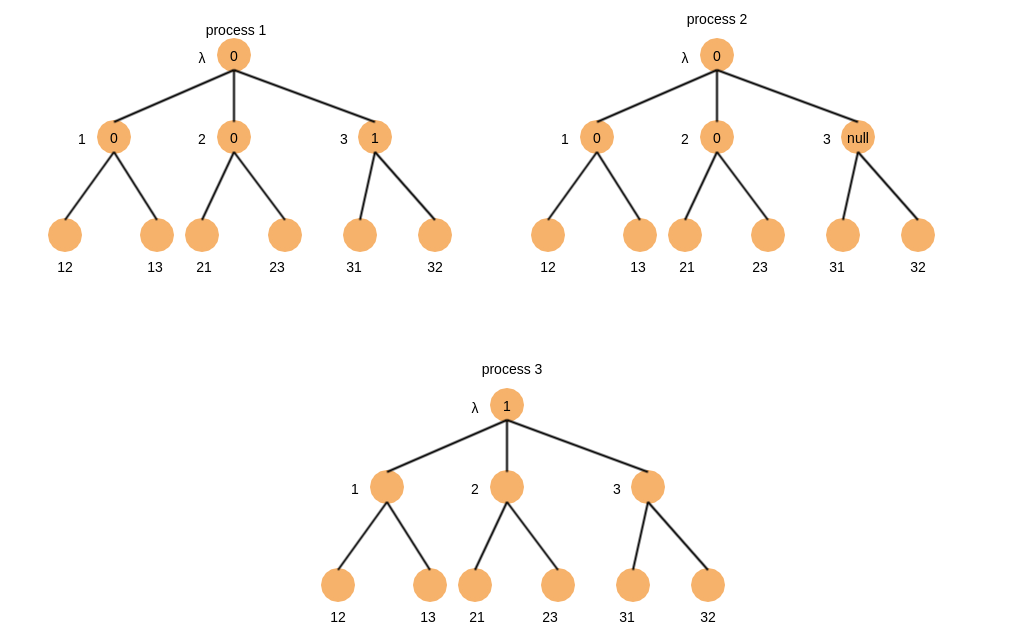
3. round=2，可以观察到进程2从进程1处获取了进程3的初始值
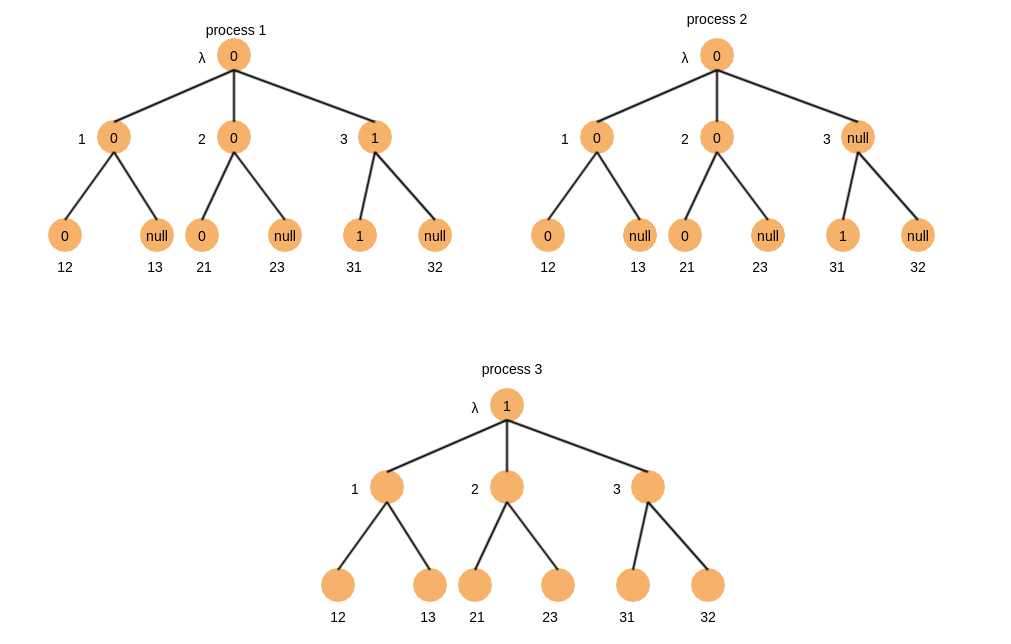
复杂度分析
1. 时间复杂度：$f+1$
2. 通信复杂度：通信次数复杂度$O((f+1)n^2)$，通信位数复杂度$O(n^{f+1}b)$，和故障数呈指数关系

Byzantine故障

Byzantine故障是什么

背景：拜占庭帝国派出10支军队去攻打一个城池，只有当6支军队同时发起进攻，才能攻破城池。将军之间依靠信使通信传递进攻方案，我们假设信使是忠诚的，但是有些将军可能是内奸。比如A,B两个将军发起进攻的方案决议，内奸可能会同意A的方案，转头又同意B的方案；或者假装不回应，因此需要多次通信来确保没有一个将军是同意了不同提议者的方案

EIGByz算法

如果节点$n \le 3*f$，那么不可能达成一致，比如3个节点中有一个节点是叛徒，那么另外两个节点无法判断哪个是真
EIGByz决议规则
1. 如果是叶子节点，$newval(x) = val(x)$
2. 如果是非叶子节点，$newval(x)$等于子节点多数值，否则为默认值$v_0$
EIGByz算法例子，EIG算法上边已描述，接下来是一个简单的例子，假设有4个节点，其中有一个节点是叛徒
- 下边是结构为$T_{4,1}$的EIG Tree，假设进程3是叛徒，在第一轮中，进程3告诉进程1说他的值为0，但是进程3告诉进程2、4它的值为1，在第二轮中，进程3又告诉进程说进程1告诉它进程1的值为0，并且说进程2告诉它进程2的值为0；在进程2中，进程3告诉进程2说进程1告诉它的值为0；在进程4中，进程3告诉进程4说进程4告诉它的值为1
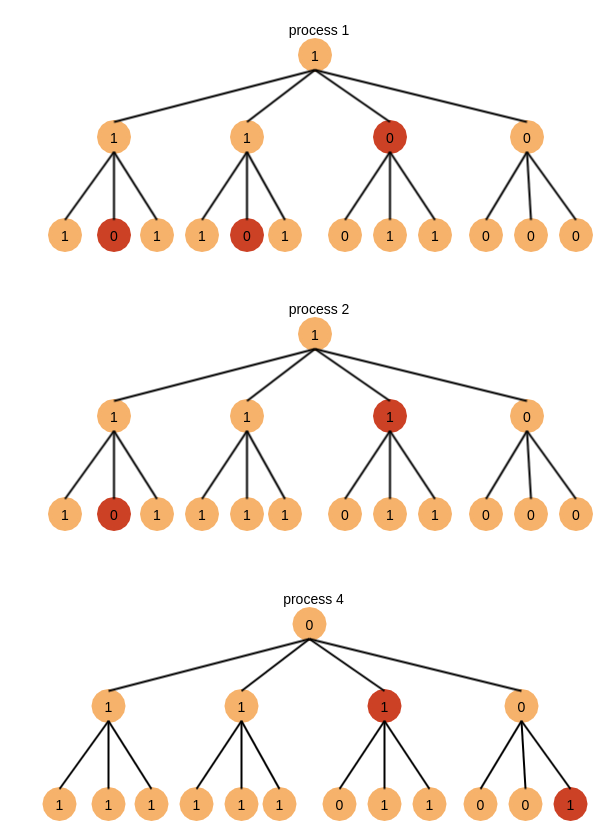
- 根据决议规则，结果如下，根据多数规则决议，最终进程1、2、4达成一致
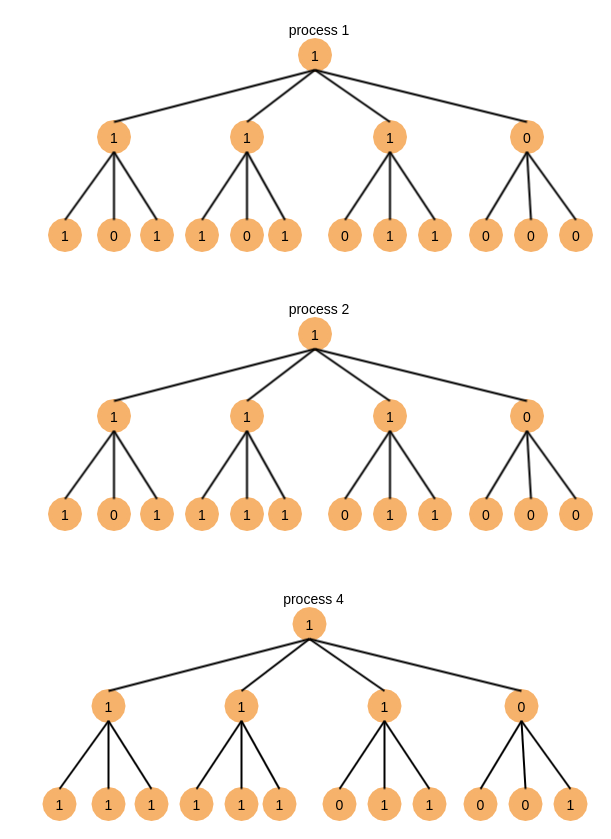
定理
1. 定理1：EIGByz算法在f+1轮之后，如果i、j、k是诚实进程，那么所有以k结尾的label x都满足$val(x)_i = val(x)_j$
  - 证明：如果k是正常诚实进程，那么它发送给i和j的消息是相同的
2. 定理2：EIGByz算法在f+1轮之后，假设lebel x结尾的进程是非故障进程，那么有一个$v \in V$满足$val(x)_i = newval(x)_i= v$对任意非故障进程i成立
  - 证明
    1. 叶子节点：根据定理1，在f+1轮后，所有以非故障进程结尾的lebel x满足$val(x)_i = val(x)_j$，并且根据叶子节点的决议规则$newval(x) = val(x)$，因此定理2得证
    2. 非叶子节点：因为非叶子节点的$newval(x)$根据子节点的多数$newval$决定的，上边已经证明了它们以正常进程结尾的子节点的值是相同的，那么我们可以得到它们的多数值是相同的，因为我们开始提过$n>3f$，所以在任意的r轮中，其子节点数为$n-r$，$n-r > n-f$这个是无疑问的，所以$n-r$是大于$2f$的，因为正常节点是大于$f$的，所以大多数值为真实值
3. 定理3：如果所有非故障进程的初始值相同$v \in V$，那么$v$是非故障进程最终唯一的决议值
  - 证明：因为所有非故障节点初始值相同为$v$，因此在第一轮通信后对于任意的进程i存在$val(j)_i=v$相同，根据定理2，那么$newval(j)_i = val(j)_i=v$相同，根据多数投票决议，那么$newval(\lambda)=v$
4. 定理4：存在一条覆盖路径包含的节点全是Common node
  - Path covering：一个EIG Tree的子集，这个子集至少包含EIG Tree每一条路径中的一个节点比如下图的红色标记的节点$(1,21,23,24,3,4)$
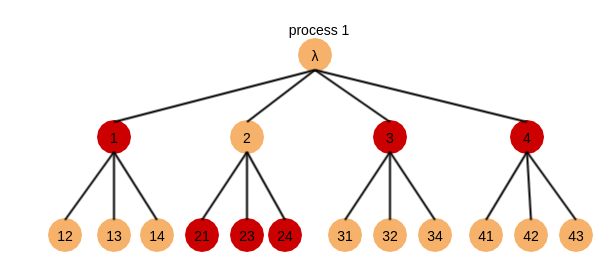
  - Common node：如果一个EIG Tree节点在所有非故障进程的有相同的$newval$值，那么它就是Common node
  - 证明：根据定理2，如果一个节点label以一个非故障节点结尾，那么它是一个common node，一条路径从root到leaf节点有f+1个节点，并且每一个节点都是从不同进程发送来的消息，总的故障节点最多有f个，因此每条路径都至少有一个是非故障进程发送来的消息，因此只要选出每条路径上的这个节点就可以组成一个覆盖路径的节点全是common node

总结

本篇文章主要讲了在分布式同步网络环境中，通信故障和节点故障发生时如何保证系统的一致性，当然一致性算法肯定不止这些，有机会会多介绍一些。