日常随笔-3-谈查找算法

引言

计算机处理数据无外乎是两种方式，一种是查询，第二种是修改。本文主要讨论的是查询这一操作，在查询数据时，我们最容易想到的方式那就是顺序查找，就遍历一遍呗，直到找到匹配的数据，那么时间复杂度是$O(n)$，当数据规模不大时，这么查找也没啥问题，但是一旦数据规模较大时，那么查询的时间就会变得很慢。这时候就有一些高效算法出来了，比如hash、内存中二分查找、存储引擎中的B+Tree，本文就详细介绍一下这些算法

查找算法

Hash表

• 定义：hash表又叫散列表，通过一个hash函数把任意长度的输入转换为相同长度的输出，通常输出为数值类型，然后通过输出数值做一些操作映射到对应的数组中。查询的时候就是查询的值通过hash函数转换为输出的数值，然后通过这个值找到在数组中对应的下标，从而达到快速查找的目的

• hash冲突

  从上边可以看到hash表的核心就是hash函数的选择，如果hash函数选择的不好，会导致大量的hash冲突，简单举个例子，如果让你来设计一个hash函数你会怎么设计呢？你可能会设计

  • 输入是个数值，那就直接输出该数值即可
  • 输入是个字符串，那么我们可以累加字符的值，将和作为输出，比如abc，它们的hashcode为294，细心的你可能已经发现这个算法很容易发生冲突，比如acb、bac、bca的hashcode都是294，为什么会这样呢？是因为我们的hash算法只考虑了字符的数量，而没有考虑字符的位置信息，如果加入位置信息就可以更好的散列，减少冲突。当然本文的目的不是讲解hash函数算法，这里只是想介绍一下hash表的使用过程。

  即使hash函数选择的再好，也不能消除冲突，因为hash表建立在数组之上，是利用了hashcode的操作映射到对应的hash槽中也就是数组元素通过数组的下标随机访问来实现快速查询，因为数组不可能无限大，冲突无法避免。

  • 解决hash冲突

    • 拉链法，这种方法被广泛使用，它的原理是发生hash冲突时，采用链表来存储冲突的元素，如下图

      

    • 开放地址法，采用一个数组来存储，当发生冲突时，探测其他位置，比如线性探测，当发生hash冲突时探测后一个位置是否可以用

      $$hash(key) = (hash_1(key) + i) \%n$$

• 特点：适合用于精确查询，不适合范围查询

• 应用

  • key-value键值对存储和查询，适用于缓存，提升查询速度
  • Mysql中的hash索引
  • Java中的hashmap
  • 算法设计时，需要用到在$O(1)$时间复杂度内查询，比如DP的备忘录，two sum

二分查找

• 原理：二分查找针对的数据是有序的数据，假设数据是升序的，每次用中间值和目标值对比，如果和目标值相同，那么返回；如果中间值小于目标值，那么丢弃左区间，查询右区间；如果中间值大于目标值，那么丢弃右区间，查询左区间

• 查找时间复杂度：$O(\log_2n)$，推导过程

  1. 从原理中了解到每次查找都排除一半，因此第一次

     $$residue = \frac{n}{2^1}$$

  2. 第二次

     $$residue = \frac{n}{2^2}$$

  3. 当最后剩余数据为1个时，那么就停止了

     $$residue = \frac{n}{2^m}$$

     当residue=1，那么$\frac{n}{2^m}=1$，那么$m=\log_2n$，所以查询时间复杂度为$O(\log_2n)$

• 特点：适用于有序的数组查询

• 应用

  • 有序数组查询目标值

二叉查找树

• 原理：最简单和最容易想到的是顺序查找，其次想到的是有序的数据可以用二分查找，有些数据是有序，但是它需要频繁的插入和删除，这个时候数组就不合适。我们知道链表可以高效的插入和删除，但是链表不支持二分查找，因此诞生了二分查找树，结构如下图

  

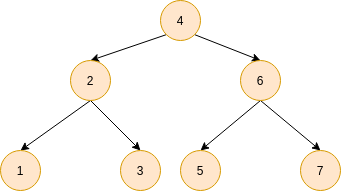
• 查找时间复杂度：$O(\log_2n)$，和二分查找一样，但是插入的顺序可能导致树结构退化成链表，可以用平衡二分查找树来避免，比如红黑树

• 特点：适用于有序的数据查询，并且插入和删除频繁，一般用于内存中做查找

• 应用

  • Linux线程调度器
  • epoll内核维护监听的句柄
  • Java的hashmap中当节点一个桶的结果数超过8时会转换成红黑树结构

SkipList

• 原理：虽然红黑树是一种平衡树，在查找性能是比较高，但是删除和插入节点时因为要考虑的情况比较多，实现还是不简单，skiplist可以提供近似的$O(log_2n)$的查找时间复杂度，并且高效的支持范围查询，并且实现比较简单，接下来我们看一下skiplist的结构，当插入一个节点时，我们是以概率的方式来决定是否需要向上延伸，假设概率为p

  

• 最大高度推导，我们知道当该层节点数最多为1时肯定是最上层

  1. 一个节点在l层有节点的概率为$p^{l-1}$
  2. 在l的节点数期望为$n*p^{l-1}$
  3. 所以l层为最上层的条件需要满足$n*p^{l-1} = 1$，那么$n=(\frac{1}{p})^{l-1}$，$l=\log_{(\frac{1}{p})}n+1 = \log_{(\frac{1}{p})}n$

• 查找时间复杂度推导，可以采用逆向思考的方式来，从目标值出发，要经过多长路径可以到达最长层，假设用C(l)代表从0层爬到l层的经过路径的期望，在任意一个节点，有p的概率向上移动，有1-p的概率向左移动

  1. 已知$C(0)=0$

  2. 根据上边的描述，那么到达l层有两种可能，从下层或者同层右边

     $$C(l) = p(1+C(l-1)) + (1-p)(1+C(l)) = C(l–1) + 1/p$$

     可以看到是一个等差数列，所以

     $$C(l) = \frac{l}{p}$$

     将上边求得的l带入式子，则查找时间复杂度为$\frac{\log_{(\frac{1}{p})}n}{p}$，将p=1/2带入式中化简为$O(logn)$

• 特点

  • 基于概率模型
  • 实现比红黑树简单的多，并且提供了和红黑树相似的查找时间复杂度
  • 可以提供高效的范围查询，只需要找到开始节点然后遍历就可以完成

• 应用

  • redis中使用了skiplist来实现zset
  • java中使用了skiplist实现并发hashmap

B+Tree

• 原理：B+Tree也是一个树型的查找数据结构，和二叉查找树类似，但是B+Tree是多叉树，一个节点内有多个key，我们称为度，其结构如下

  

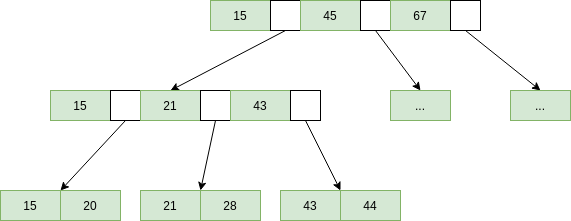
• 查找时间复杂度：先放结论，$O(log_2n)$，接下来是推导

  1. 假设有n个key，每个节点可以存放m个可以，那么我们很容易推导到树的高度为$log_mn$

  2. 每个节点内的查询复杂度是什么呢，我们知道节点内的key是有序的，因此可以用二分查找，所以节点内查询时间复杂度为$log_2m$

  3. 因此B+Tree查找时间复杂度是$高度每层查找复杂度$，因此$log_2mlog_mn$，化简

     $$log_2m*log_mn = log_2m*\frac{log_2n}{log_2m} = log_2n$$

• 特点：因为其一个节点存储多个key是多叉树，因此具有相同数量key的B+Tree比二叉查找树的高度低得多，这个有什么作用呢？其实有很大的用处，当数据需要持久化存储时，那么必须存在磁盘上，我们知道访问磁盘是很慢的，我们在查找数据的过程中必须要减少磁盘的io次数，而二叉查找树因为高度较高，因此需要更多的磁盘io，所以不适合用来在磁盘上构建查找的数据结构，B+Tree就比较适合

• 应用

  • 各类数据库的索引，比如MySQL，默认B+tree的节点空间为16kb，64位系统指针是8byte，如果我们假设关键字key为long类型占用8个字节，那么我们可以估算一个节点可以存放的key大约为1024个，那么假设B+tree高度为3，那么可以存储的key为大约为10亿

总结

本文大概讲了一些用于查找的算法，因为是想到什么写什么，肯定还有很多是没有想到的，欢迎大家补充。大家也可以关注我的公众号，一起学习